Materials
Raney iron precursor
Iron-aluminium alloy powder (50:50 by weight, Sigma-Aldrich) was added into an 8âmolâlâ1 KOH (AR, Sinopharm Chemical Reagent) solution in a flask under stirring and heated to 70â°C to dissolve the aluminium in the alloy36,37. Afterwards, K+ and \({{\rm{AlO}}}_{2}^{-}\) ions were removed by washing with deionized water (ten times) and ethanol (seven times). The iron powder sample was transferred by means of a sealable quartz tube into a glove box and subsequently dried in an argon flow at room temperature for 6âh. The resulting porous iron powder was kept in a container with a seal in a glove box. Before loading the sample in appropriate in situ cells (XRD and Mössbauer spectroscopy characterization) or a stainless-steel reactor for FT activity measurements, the sample was passivated in a flow of 1% O2 in helium at room temperature for 20âh.
Manganese-Raney iron precursor
Manganese (0.5â12.5âwt%) was added to the Raney iron precursor (directly after removal of aluminium) by wet impregnation using a Mn(NO3)2 solution. The sample was then dried in a vacuum oven at room temperature for 12âh.
Potassium-Raney iron precursor (Extended Data Fig. 3c)
Potassium (1âwt%) was added to the Raney iron precursor (directly after removal of aluminium) by wet impregnation using a KNO3 solution. The sample was then dried in a vacuum oven at room temperature for 12âh.
Characterization
In situ X-ray diffraction (in situ XRD) was carried out on a Rigaku D/max-2600/PC instrument equipped with a D/teX ultrahigh-speed detector and scintillation counter. The X-ray generator consisted of a copper rotating anode with a maximum power of 9âkW. All measurements were carried out at 40âmA and 40âkV. In situ XRD patterns were recorded in an Anton Par XRK-900 cell equipped with a CO/H2/Ar gas inlet system.
Environmental TEM (ETEM) images were recorded in an aberration-corrected FEI Titan ETEM G2 instrument at an acceleration voltage of 300 kV (ref.â38). Syngas was introduced for 1âh under 1,200âPa at 320â°C as a pretreatment. The carburization temperature was then raised to 350â°C in about 0.5âh, followed by monitoring the sample continuously.
In situ Mössbauer spectroscopy was carried out in an in situ high-pressure cell suitable for Mössbauer spectroscopy39. Transmission 57Fe Mössbauer spectra were collected at â153â°C with a sinusoidal velocity spectrometer using a 57Co(Rh) source. The source and the sample were kept at the same temperature during the measurements. Mosswinn 4.0 software was used for spectra fitting40.
Catalytic activity measurements
In situ carburization of Ï-Fe5C2 and Mn-Ï-Fe5C2 and FTLAO catalytic activity measurements
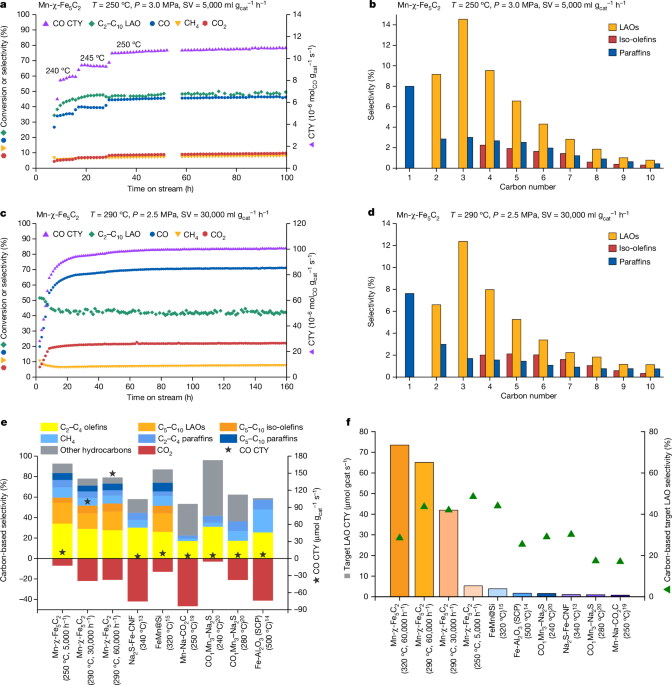
A 75âmg amount of Raney iron precursor or manganese/Raney iron precursor, the latter also containing 75âmg of Raney iron, was diluted with 1,500âmg silicon carbide and loaded into a stainless-steel tubular fixed-bed reactor with an external diameter of 14.5âmm, internal diameter of 9âmm, length of 305âmm and total internal volume of 20âml. An exception was the test in Table 1, row 1, for which 225âmg Raney iron of a manganese-Raney iron precursor was diluted with 4,500âmg silicon carbide to achieve a low SV of 5,000âmlâ\({{\rm{g}}}_{{\rm{cat}}}^{-1}\,{{\rm{h}}}^{-1}\). The catalyst precursor was in situ carburized in a syngas flow (H2/CO/He = 100/3.2/21.8) while increasing the temperature to 350â°C at a rate of 1â°Câminâ1, followed by a dwell of 6âh at ambient pressure and an SV of 75,000âmlâ\({{\rm{g}}}_{{\rm{cat}}}^{-1}\,{{\rm{h}}}^{-1}\). After cooling the reactor to 250â°C (240â°C for the test in Table 1, row 3), the reactor feed was switched to the feed mixture and the reactor pressure was increased to the desired value. The start of the reaction was defined as the time at which these conditions were reached. The reactor was then ramped to the indicated temperature.
For the comparison between Ï-Fe5C2 and Mn-Ï-Fe5C2 (Table 1, rows 1 and 2), the reaction conditions were as follows: a feed mixture SV of H2/CO/Heâ=â12,000/8,000/8,000âmlâ\({{\rm{g}}}_{{\rm{cat}}}^{-1}\,{{\rm{h}}}^{-1}\)), a reaction pressure of 2.3âMPa and a reaction temperature of 250â°C. For the evaluation of the Mn-Ï-Fe5C2 catalyst under different temperatures and pressures (Fig. 1aâf and rows 3â6 of Table 1), the reaction conditions were as follows: a feed mixture of H2/CO/Ar (internal standard)â=â1.5/0.95/0.05 at a total SV of 5,000, 30,000 or 60,000âmlâ\({{\rm{g}}}_{{\rm{cat}}}^{-1}\,{{\rm{h}}}^{-1}\), a reaction pressure of either 2.5 or 3.0âMPa and a reaction temperature of 250, 290 or 320â°C (heating rate 0.1â°Câminâ1). For the evaluation of the Mn-Ï-Fe5C2 catalyst in Extended Data Table 2, the reaction conditions were as follows: a feed mixture SV of H2/COâ=â1.5 at a total SV of 30,000, 60,000, 75,000 or 90,000âmlâ\({{\rm{g}}}_{{\rm{cat}}}^{-1}\,{{\rm{h}}}^{-1}\) with no inert gas added, a reaction pressure of 2.5âMPa and a reaction temperature of 250, 270, 290 or 310â°C (heating rate 0.1â°Câminâ1). For the evaluation of Mn-Ï-Fe5C2 (Extended Data Fig. 5a) and K-Ï-Fe5C2 (Extended Data Fig. 3c), the reaction conditions were as follows: a feed mixture SV of H2/CO/Heâ=â36,000/24,000/24,000âmlâ\({{\rm{g}}}_{{\rm{cat}}}^{-1}\,{{\rm{h}}}^{-1}\) or 72,000/48,000/48,000âmlâ\({{\rm{g}}}_{{\rm{cat}}}^{-1}\,{{\rm{h}}}^{-1}\) and a reaction pressure at 2.3âMPa. The reaction temperature was 315 or 325â°C for these measurements (heating rate 0.5â°Câminâ1). For the long-term test for Mn-Ï-Fe5C2 (Extended Data Fig. 5c), the reaction conditions were as follows: a feed mixture SV of H2/CO/Heâ=â60,000/40,000/40,000âmlâ\({{\rm{g}}}_{{\rm{cat}}}^{-1}\,{{\rm{h}}}^{-1}\) and a reaction pressure at 2.3âMPa. We used a low ramp rate of 2â°Câhâ1 to avoid overheating issues due to the exothermicity of the reaction. Therefore, it took 35âh to raise the temperature from 250â°C to 320â°C.
The effluent gas flow was analysed by an online Agilent 7890 gas chromatograph equipped with two thermal conductivity detectors and one flame ionization detector. Each result was acquired from a single experiment. All of the SVs are calculated on the basis of the weight of the Raney iron catalyst precursor without a promoter or silicon carbide diluent.
The CO conversion and product selectivity were calculated as below.
The CO conversion (\({X}_{{\rm{CO}}}\)) was calculated by
$${X}_{{\rm{CO}}}=\frac{{{\rm{CO}}}_{{\rm{inlet}}}-{{\rm{CO}}}_{{\rm{outlet}}}}{{{\rm{CO}}}_{{\rm{inlet}}}}\times 100 \% $$
(1)
The CO2 selectivity (\({S}_{{{\rm{CO}}}_{2}}\)) was calculated by
$${S}_{{{\rm{CO}}}_{2}}=\frac{{{\rm{CO}}}_{{2}_{{\rm{outlet}}}}}{{{\rm{CO}}}_{{\rm{inlet}}}-{{\rm{CO}}}_{{\rm{outlet}}}}\times 100 \% $$
(2)
The carbon-based hydrocarbon selectivity (\({S}_{{{\rm{C}}}_{x}{{\rm{H}}}_{y}}\)) was calculated by
$${S}_{{{\rm{C}}}_{x}{{\rm{H}}}_{y}}=\frac{{x{{\rm{C}}}_{x}{{\rm{H}}}_{y}}_{{\rm{outlet}}}}{{{\rm{CO}}}_{{\rm{inlet}}}-{{\rm{CO}}}_{{\rm{outlet}}}}\times 100 \% $$
(3)
The indicated parameters represent the inlet and outlet molar flows determined.
The CO catalyst time yield (\({{\rm{CTY}}}_{{\rm{CO}}}\)) was calculated by
$${{\rm{CTY}}}_{{\rm{CO}}}=\frac{{{X}_{{\rm{CO}}}\times {\rm{CO}}}_{{\rm{inlet}}}}{\mathrm{22,400}\,({\rm{ml}}\,{{\rm{mol}}}^{-1})\times \mathrm{3,600}\,({\rm{s}}\,{{\rm{h}}}^{-1})}$$
(4)
The carbon-based hydrocarbon catalyst time yield (\({{\rm{CTY}}}_{{{\rm{C}}}_{x}{{\rm{H}}}_{y}}\)) was calculated by
$${{\rm{CTY}}}_{{{\rm{C}}}_{x}{{\rm{H}}}_{y}}={{\rm{CTY}}}_{{\rm{CO}}}\times {S}_{{{\rm{C}}}_{x}{{\rm{H}}}_{y}}$$
(5)
The experimental chain-growth probability was calculated by the ASF distribution as follows
$${\rm{ln}}\left(\frac{{W}_{n}}{n}\right)=n{\rm{ln}}\alpha +{\rm{ln}}[{\left(1-\alpha \right)}^{2}/{\alpha }]$$
(6)
in which n is the number of carbon atoms in a particular hydrocarbon product, Wn is the weight fraction of a product with n number of carbon atoms and α is the chain-growth probability.
Theoretical modelling
Density functional theory calculations
Density functional theory (DFT) calculations were carried out to obtain the energetics for elementary reaction steps relevant to the FT reaction on Ï-Fe5C2. All spin-polarized DFT calculations were conducted using the projector augmented-wave method and the PerdewâBurkeâErnzerhof functional, as implemented in the Vienna ab initio simulation package code. Solutions of the KohnâSham equations were obtained using a basis set of plane waves with a cutoff energy of 400âeV. Sampling of the Brillouin zone was carried out using a 5âÃâ5âÃâ1 k-point mesh. Higher cutoff energies or a finer Brillouin zone sampling did not lead to substantial energy differences. All atoms were allowed to relax during the optimization of the empty surfaces. We used a 2âÃâ2âÃâ1 unit cell for the (100) surface, containing 80âiron and 32âcarbon atoms, with a layer thickness of 10.31âà . A vacuum layer of 15âà was added perpendicular to the surface to avoid spurious interactions between neighbouring images. Adsorption of atoms and molecules was carried out on the top side of the slab, whereas the lower half was frozen. A dipole correction was carried out for all adsorbed states. Further technical details such as Vienna ab initio simulation package settings for these iron carbide calculations are described elsewhere23. The adsorption energies of the gas-phase molecules were determined by subtracting the energies of the empty surface and the free adsorbate from the adsorbed state. The energy of the adsorbate in the gas phase was obtained by placing a molecule at the centre of a 10âÃâ10âÃâ10 à 3 unit cell, using the Î-point for k-point sampling. Transition states were acquired using the nudged elastic band method41. A frequency analysis was carried out to confirm that all transition geometries correspond to a first-order saddle point on the potential energy surface with an imaginary frequency in the direction of the reaction coordinate. The corresponding normal-mode vibrations were also used to calculate the zero-point energy correction. We also corrected the barriers for the migration of fragments after dissociation by considering the energy difference of the geometry directly after dissociation and their most stable adsorption positions at infinite distance.
We carried out DFT calculations to determine the energetics of elementary reaction steps of the conversion of synthesis gas into hydrocarbons (methane, olefins and paraffins) and CO2 and H2O. The energy barriers and their corresponding pre-exponential factors are listed in Extended Data Table 1. The (100) surface of Ï-Fe5C2 was selected, because this surface is a stable surface termination of Hägg carbide and also allows for facile CâO bond dissociation, which is an essential step in the FT reaction42. Extended Data Table 1 shows forward and backward activation energies and the corresponding pre-exponential factors for the consecutive hydrogenation steps of adsorbed carbon to methane and the removal of oxygen as H2O and CO2. Extended Data Table 1 shows forward and backward activation energies and the corresponding pre-exponential factors for the CâC coupling reactions and the hydrogenation to ethylene and ethane.
Microkinetics modelling
For the construction of the microkinetic model of the FT reaction, differential equations for all reaction intermediates on the catalytic surface were constructed using the rate constants of all considered elementary reaction steps. Herein, we assumed that all adsorbates occupy one active site. For adsorption, we assumed that the adsorbate loses one translational degree of freedom in the transition state with respect to the initial state. For desorption, we assumed that the species gains two translational degrees of freedom and three rotational degrees of freedom in the transition state with respect to the initial state. From these two assumptions, the rate of adsorption and desorption are as follows:
$${k}_{{\rm{ads}}}=\frac{P\times A}{\sqrt{2{\rm{\pi }}\times m\times {k}_{{\rm{B}}}\times T}}$$
(7)
$${k}_{{\rm{des}}}=\frac{{k}_{{\rm{B}}}\times {T}^{3}}{{h}^{3}}\times \frac{A\times \left(2{\rm{\pi }}\times m\times {k}_{{\rm{B}}}\right)}{\sigma {\theta }_{{\rm{rot}}}}\times {{\rm{e}}}^{\frac{{E}_{{\rm{des}}}}{RT}}$$
(8)
Herein, \({k}_{{\rm{ads}}}\) is the rate constant for the adsorption of the adsorbate, P is the pressure in pascals, A is surface area in square metres, m is the mass of the reactant in kilograms, kB is the Boltzmann constant in joules per kelvin, T is the temperature in kelvin, \({k}_{{\rm{des}}}\) is the rate constant for the desorption of the adsorbate, h is the Planck constant in joules multiplied by seconds, \(\sigma \) is the symmetry number, \({\theta }_{{\rm{rot}}}\) the rotational temperature in kelvin, Edes is the desorption energy in joules per mole, and R is the gas constant in joules per kelvin per mole.
The rate constant (k) of an elementary reaction step was determined using the Eyring equation, which is defined as follows:
$$k=v{\text{exp}}^{\left(\frac{-{E}_{{\rm{act}}}}{{k}_{{\rm{B}}}T}\right)}$$
(9)
in which \({E}_{{\rm{act}}}\) is activation energy in joules per mole, kB the Boltzmann constant, T the temperature in kelvin, and \(v\) the pre-exponential factor in the unit of per second. Pre-exponential factors for the forward and backward reactions can be obtained using:
$${v}_{{\rm{forward}}}=\frac{{k}_{{\rm{B}}}T}{h}\left(\frac{{q}_{{\rm{vib}}}^{{\rm{TS}}}}{{q}_{{\rm{vib}}}^{{\rm{IS}}}}\right)$$
(10)
and
$${v}_{{\rm{backward}}}=\frac{{k}_{{\rm{B}}}T}{h}\left(\frac{{q}_{{\rm{vib}}}^{{\rm{TS}}}}{{q}_{{\rm{vib}}}^{{\rm{FS}}}}\right)$$
(11)
in which \({v}_{{\rm{forward}}}\) and \({v}_{{\rm{backward}}}\) refer to the pre-exponential factors for the forward and the backward reaction, respectively, qvib is the vibrational partition function of the initial state (IS) and the transition state (TS), and h is Planckâs constant.
All microkinetic simulations were carried out using the MKMCXX software suite43. The set of differential equations were time-integrated using the backward differentiation formula method until a steady-state solution was obtained. From the steady-state coverages, the rates of the individual elementary reactions steps were obtained using a flux analysis, as implemented in the MKMCXX software. To mimic experimental conditions, the pressure was set to 0.1âMPa over a temperature range between 510âK and 545âK. We adopted a continuously stirred tank reactor with ideal mixing using an SV chosen to obtain differential conditions over the whole temperature range. The H2/CO ratio was kept constant at 2:1. Chain growth was considered by involving coupling of two CHx adsorbates. Chain growth for hydrocarbon chains up to 20 carbon atoms was considered by treating the growing chain as CR, in which Râ=âalkyl chain and considering that barriers for chain growth are independent of chain length. Adsorption energies of C2 and C3 intermediates were taken into account explicitly, whereas those of hydrocarbon fragments with more than three carbon atoms were taken to be equal to those of C3 intermediates. Proper entropy corrections were made depending on the chain length of the hydrocarbons.
The chain-growth probability was determined from the ASF distribution by considering hydrocarbon products containing 1â20 carbon atoms:
$${\alpha }=\frac{{r}_{{\rm{p}}}}{{r}_{{\rm{p}}}+{r}_{{\rm{t}}}}\cong \exp \left(\frac{{\rm{d}}{\rm{ln}}{F}_{{{\rm{C}}}_{n}}^{{\rm{out}}}}{{\rm{d}}n}\right)$$
(12)
Herein, the chain-growth probability is defined as the rate of propagation (\({r}_{{\rm{p}}}\)) over the sum of the rates of propagation and termination (\({r}_{{\rm{t}}}\)). \({F}_{{{\rm{C}}}_{n}}^{{\rm{out}}}\) corresponds to the flow rate of \({C}_{n}\) in the experiment. This involved simulating the corresponding chain-growth probability (α) and C2 selectivity within the ASF distribution shown in Extended Data Fig. 2.
Results of microkinetic simulations
Extended Data Fig. 1a shows the CO conversion rate and formation rates of CH4 (C1) and longer hydrocarbons (C2+) for the (100) surface of Ï-Fe5C2 as a function of temperature. As expected, the rates exponentially increase with temperature owing to the Arrhenius dependence of the reaction rate constants. The CO conversion rate is in the same range as experimentally observed for iron carbide catalysts42,44. The selectivity towards CH4 is lower than the total selectivity towards other hydrocarbons, which is important because CH4 has a much lower value than higher hydrocarbons. Extended Data Fig. 2a shows the hydrocarbon product distribution, which indicates that, except for C1 and C2, the longer hydrocarbons are statistically distributed according to the ASF theory. The parameter describing this distribution is the chain-growth probability and its temperature dependence is shown in Extended Data Fig. 2b. This parameter reflects the statistical nature of the growth process in which hydrocarbons can either grow by addition of a C1 monomer or desorb as a product. The decrease with temperature shows that termination as products has a higher overall activation energy than chain growth. The value of about 0.5 is slightly lower than experimentally observed in our study. Extended Data Fig. 2c shows the simulated O/P ratio to be around 3.0 with a minor dependence on temperature. These data show that both olefins and paraffins are formed as primary products. The O/P values are in the same range as experimentally observed, namely about 1.5 for the unpromoted catalyst and about 3.6 for the manganese-promoted catalyst. Extended Data Fig. 1b demonstrates that oxygen atoms originating from CO dissociation are predominantly removed as H2O, instead of CO2. These findings provide an explanation for the low CO2 selectivity observed in our experimental study in which a pure Ï-Fe5C2 catalyst was used. In other studies in which the catalyst precursor is not completely converted to Ï-Fe5C2, competing phases often include iron oxides, which are known as good catalysts for the (reverse) waterâgas shift reaction.
The computational predictions in Extended Data Table 1 show that, on Ï-Fe5C2, the overall barrier for H2O formation (155âkJâmolâ1) is lower than the barrier for CO2 formation (181âkJâmolâ1). This implies that H2O formation is preferred on Ï-Fe5C2 over CO2 formation as the oxygen removal step. To verify this prediction based on the overall energy barrier under reaction conditions, we used microkinetic simulations based on DFT-based reaction energetics and found that oxygen removal reactions proceed primarily through the formation of H2O (99.4% at 525âK) instead of CO2 (0.6% at 525âK; Extended Data Fig. 1c). These simulations showing a very low CO2 selectivity pertain to the zero-conversion limit and, thus, represent so-called primary CO2 production. The microkinetic simulations also provide a deeper insight into the reaction mechanism including the interplay between the surface intermediates. In Extended Data Fig. 1d we show that, in addition to CO dissociation, oxygen removal and carbon hydrogenation (as part of the chain-growth mechanism) control the overall reaction rate. These findings are in keeping with the periodic trends predicted in previous work43.
Rietveld refinement XRD patterns
The results of Rietveld refinement of the XRD patterns using the Fullprof software are shown in Extended Data Fig. 7g. Rietveld refinement confirmed the phase purity of Ï-Fe5C2 (no substantial contribution of other phases) with a goodness of fit of Ï2â=â7.58%, Rpâ=â18.7%, Rwpâ=â15.3% and Rexpâ=â5.6%. The space group and lattice parameters listed in Extended Data Fig. 7g are in good agreement with published data for Ï-Fe5C2 (ref.â45). The atomic positions of the specific sites for the Ï-Fe5C2 structure are listed in Extended Data Fig. 7h. Note that the data were acquired in an in situ XRD reaction chamber under a nitrogen flow after obtaining the Ï-Fe5C2 particles through the described synthesis method.